
By Josh Feldman
The dog days of winter hit me hard this year as cabin fever hit many of us here in the heartland. I needed something to take my mind off the ice outside and find something to look forward to. And then my brother told me that the new Pokémon card game just hit mobile devices everywhere. Twice a day, you can open a free digital pack of Pokémon playing cards. My life instantaneously changed for the better!
Now, lunchtime and right before bedtime have become the most exciting time of the day; that’s when it’s time to open a new pack.
Sure, I could spend some actuarial coin to open lots more packs, and like millions of people, I have been down the social media rabbit hole of watching influencers spend tens of thousands of genuine American dollars opening a zillion packs. But opening two packs a day is all the excitement this middle-aged guy can handle.
After seeing the success of Pokémon Pocket, my friend Chef saw the lucrative side of card-collecting business and wanted to start his own digital card-collecting game. So Chef asked me for ideas on what his new card game should be about. I told him you gotta stick with what you know, and that we should create an actuarial card game, where players try to assemble the best actuarial team out there to bring each player glory and pride in the insurance sphere.
We had the game all thought out. We planned different cards for reserving actuaries, ratemaking actuaries, reinsurance actuaries, health insurance actuaries, and so on. Some actuaries would be women, some would be men, some would be old, some would be fresh out of college, and some actuaries would even have criminal arrest records. With a little bit of marketing, we could be the next internet craze, make boatloads of money, and get everyone excited about actuarial science. A true win-win-win for all!
Chef and I then settled on the details. We would create 50 actuarial training cards. Forty-five of these would be common cards, while the remaining five would be rare, special cards that would become true collectibles in the digital world. We would sell packs of five cards each. Each card in the pack would have a 99% chance of being one of the 45 common cards, and a 1% chance of being one of the five rare cards. The idea was flawless and foolproof.
While designing the cards, my brother asked me how many packs would need to open to get a complete set of all 50 actuarial cards. I told him that I was too busy working out the logistics of the trading cards to answer, but that I am sure my puzzle-solving friends would help him out.
For the following questions assume that all five cards in the pack are totally independent and random, except for the fact that each of the five cards in a pack the card has a 99% chance of randomly being one of the 45 common cards and a 1% chance of randomly being one of the five rare cards.
What is the probability that a pack has five unique cards with no duplicates?
Given the pack constraints mentioned above, what is the mean number of packs one would need to open to acquire all 50 unique cards in the set?
If we made it so that there were no rare cards, and that each of the 50 cards had an equal 2% probability of acquiring, how does this change the answer to questions 1 and 2?
Solutions may be emailed to puzzles@actuary.org.
In order to make the solver list, your solutions must be received by Apr. 1, 2025.
Solutions to Previous Puzzles—Five by Five
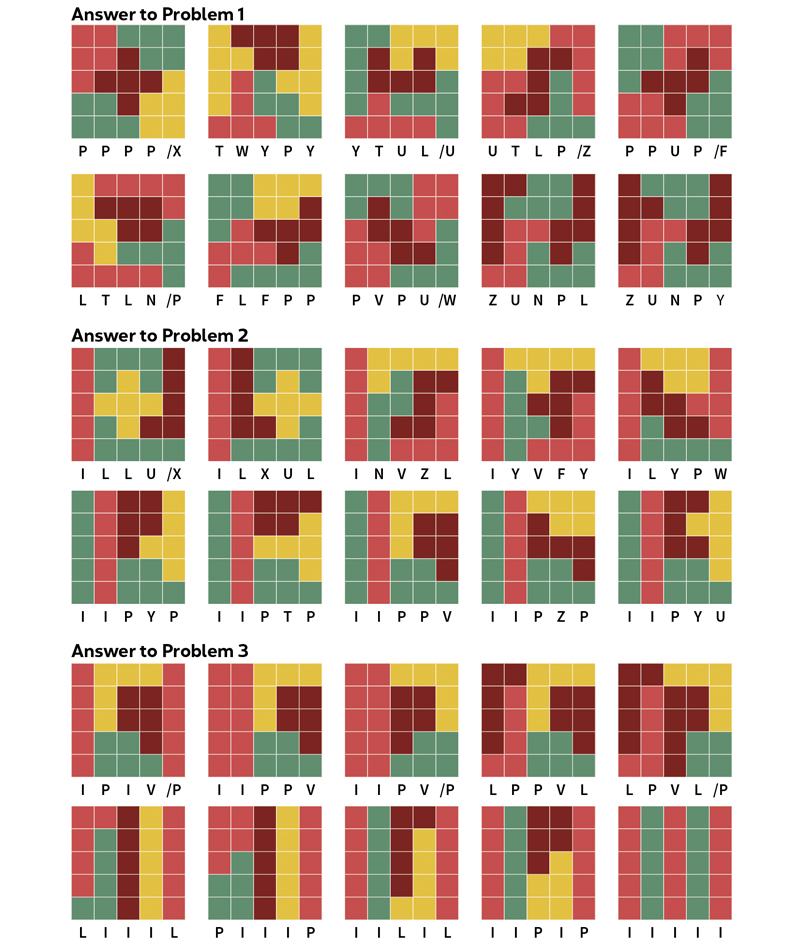
The goal of these problems was to tile 5×5 squares with 5 pentominoes. A pentomino is a polygon in the plane made up of 5 equal-sized squares connected edge to edge. We do not consider rotations and reflections to be different, so we have only 12 different pentominoes, which we label FILNPTUVWXYZ in approximate accordance with their shapes. Read the pentomino Wikipedia article for diagrams of the (non-Conway) labeling scheme we are using and a general discussion of tiling.
As with the pentominoes themselves, we do not consider rotations and reflections of tilings to be different. We split the tilings up into two classes.
Problem 1: (Class A) Find at least 10 different tilings of a 5×5 square, without using an I-tile. Also, given a pair of adjacent L-tiles (“LL”), if one rotates the second L-tile 180 degrees, lifts it up and moves it left a bit, then the resulting two L-tiles take up the same space as two adjacent I-tiles (“II”). So, we exclude that resulting configuration of L-tiles from Class A tilings. Similarly, we exclude a pair of adjacent P-tiles adjusted similarly to take up the same space as two adjacent I-tiles. On the other hand, you should include each of the remaining 11 pentominoes (other than an I-tile) in at least one of your 10 class A tilings.
Answers: One solver exhibited what they claimed to be 172 Class A tilings. In order to get a set of 10 of these, which collectively contain all 11 non-I-tiles, there is a choice of a little less than 43,051,560,438,978,234 answers: we don’t have the space to display them all. But here is one.
Solution: Trial and error works fine for all three problems.
Problem 2: (Class B) Find at least 10 different tilings of a 5×5 square, each using at least one I-tile, or a pair of L-tiles or a pair of P-tiles configured to take up the same space as a two adjacent I-tiles (“II”).
Answers: There appear to be more than 172 Class B tilings and so more than 43 quadrillion answers. Here is one.
Problem 3: Find additional tilings from either class.
Answers: Two are required. Here are 10 from Class B.
Solvers: William Darnieder, Andrew Dean, Rui Guo, David Promislow, Anna Quady, Al Spooner